Lời giải LeetCode Daily 05-07-2024
Giới thiệu
Hello xin chào mọi người, mình đã quay trở lại sau mấy ngày lặn mấy tăm đây. Trong mấy ngày qua mình vẫn giải bài tập đều đều nhưng mà không có viết lời giải và mình thấy bài của 2 ngày qua về Linked List cũng không quá khó. Do đó chúng ta sẽ tới với bài ngày hôm nay cũng về Linked List và mình đánh giá nó cũng không quá khó.
Bài toán 2181. Merge Nodes in Between Zeros
Nguyên văn bài toán như sau:
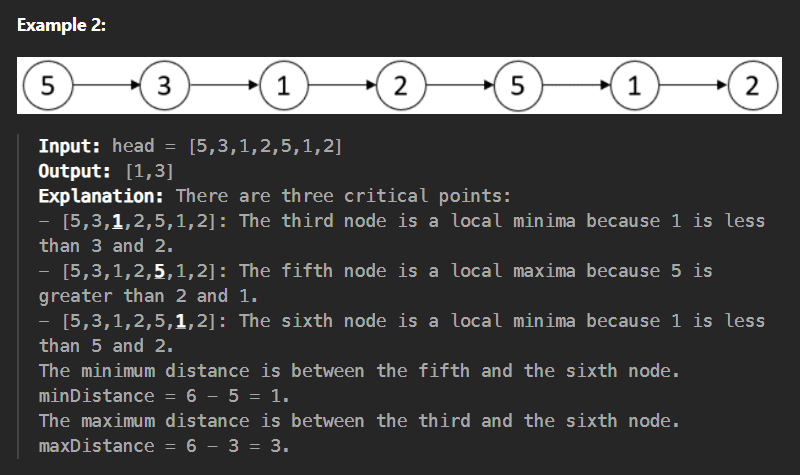
A critical point in a linked list is defined as either a local maxima or a local minima.
A node is a local maxima if the current node has a value strictly greater than the previous node and the next node.
A node is a local minima if the current node has a value strictly smaller than the previous node and the next node.
Note that a node can only be a local maxima/minima if there exists both a previous node and a next node.
Given a linked list head, return an array of length 2 containing [minDistance, maxDistance] where minDistance is the minimum distance between any two distinct critical points and maxDistance is the maximum distance between any two distinct critical points. If there are fewer than two critical points, return [-1, -1].
Tóm tắt bài toán:
- Cho một Linked list, một điểm được gọi là “critical” nếu như nó là một local maxima hay local minima (điểm này lớn hơn 2 điểm quanh nó hoặc nhỏ hơn 2 điểm quanh nó)
- Tìm khoảng cách giữa 2 điểm “critical” gần nhất và cách xa nhất
Ý tưởng
- Bài toán trên là một bài toán dạng linked list, mình sẽ giải bài toán trên thông qua sử dụng 3 con trỏ với 3 vị trí liên tiếp của một node, (thực ra bạn có thể chỉ cần sử dụng 2 con trỏ cho bài toán này thông qua phương thức
nexttrong Linked List) tuy nhiên để rõ ràng mình sẽ dùng 3 con trỏ - Thêm vào đó, để tối ưu về bộ nhớ, mình sẽ sử dụng 2 giá trị là
first- lưu index của điểm “critical” đầu tiên vàcurr- lưu index của điểm “critical” duyệt ngay trước đó. - Có thể dễ dàng thấy, khoảng cách nhỏ nhất luôn là min của khoảng cách giữa 2 điểm “critical” liên tiếp và khoảng cách xa nhất luôn là khoảng cách của điểm critical đầu tiên với điểm critical cuối cùng.
Cài đặt thuật toán
- Với ý tưởng trên, mình sẽ cài đặt thuật toán như sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def nodesBetweenCriticalPoints(self, head: Optional[ListNode]) -> List[int]:
# Kiểm tra điều kiện bắt buộc
if head == None or head.next == None or head.next.next == None : return [-1, -1]
# index tại mỗi vòng lặp
idx = 1
# 3 pointer để duyệt
pre_node = head
curr_node = head.next
nxt_node = head.next.next
# lưu index của điểm critical đầu tiên và gần nhất
first = -1
curr = 0
ans = [100000, -1]
while nxt_node != None :
# kiểm tra điều kiện để là local maxima/minima
if (curr_node.val > pre_node.val and curr_node.val > nxt_node.val) or (curr_node.val < pre_node.val and curr_node.val < nxt_node.val):
if first == -1:
first = idx
else :
# điểm min bằng min k/c giữa 2 điểm liên tiếp
ans[0] = min(ans[0], idx - curr )
curr = idx
idx += 1
pre_node = curr_node
curr_node = nxt_node
nxt_node = nxt_node.next
# điểm max luôn bằng khoảng cách từ điểm cuối tới điểm đầu
ans[1] = curr - first
# Nếu không có hoặc có 1 điểm critical
if first == curr or (first == -1 and curr == 0) : return [-1, -1]
return ans
Phân tích
- Thuật toán trên có độ phức tạp về thời gian là \(O(N)\)
- Độ phức tạp về không gian là \(O(1)\)
- Thuật toán tương đối tối ưu về cả thời gian chạy và bộ nhớ. Điểm làm thuật toán này chạy nhanh đó là do quan sát “tham lam” về các khoảng cách cực tiểu và cực đại trong Linked List
Kết luận
Đây là một bài có độ khó Medium cũng khá thú vị đúng không mọi người. Linked list luôn khó hơn với array thông thường đó là việc mình không thể truy cập trực tiếp vào vị trí của phần tử thay như array. Tuy nhiên, giới hạn này của Linked list giúp tạo ra những thuật toán, cách tiếp cận khá hay. Qua bài toán này, mình thấy việc nhận xét về bài toán ngay từ đầu khá quan trọng để cải thiện tốc độ và bộ nhớ thuật toán. Chúc mọi người một ngày mới vui vẻ!