Lời giải LeetCode Daily 28-06-2024
Giới thiệu
Đây là bài đầu tiên trong series lời giải leetcode daily của mình. Thói quen mỗi ngày làm một bài leetcode daily được mình duy trì trong khoảng thời gian dài (vẫn có mấy ngày cheat day). Mình sẽ đặt vấn đề và đưa ra lời giải của mình cho bài toán, lời giải có thể hay hoặc chưa hay, mọi người có thể đưa ra nhận xét và góp ý về email của mình 😊😊😊😊
Bài toán
Nguyên văn bài toán số 2285 như sau:
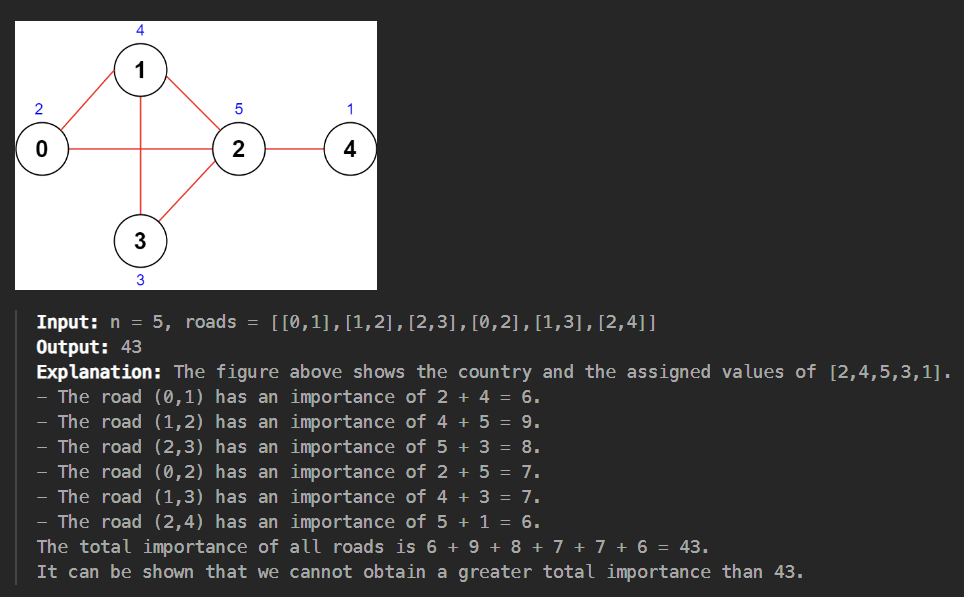
You are given an integer n denoting the number of cities in a country. The cities are numbered from 0 to n - 1.You are also given a 2D integer array roads where roads[i] = [ai, bi] denotes that there exists a bidirectional road connecting cities ai and bi. You need to assign each city with an integer value from 1 to n, where each value can only be used once. The importance of a road is then defined as the sum of the values of the two cities it connects.Return the maximum total importance of all roads possible after assigning the values optimally.
Mình có thể tóm tắt lại bài toán thành những ý sau :
- Có n thành phố được biểu diễn từ 0 -> n - 1
- Một array roads biểu diễn kết nối 2 chiều giữa hai thành phố
- Với mỗi thành phố, gán một giá trị từ 1 -> n sao cho n thành phố giá trị này không lặp lại
- Độ quan trọng của một tuyến đường là tổng giá trị vừa gán -> Tổng số độ quan trọng lớn nhất của cả tuyến đường là bao nhiêu ?
Ý tưởng
- Có thể thấy đây là một bài đồ thị yêu cầu tối ưu, các hướng tiếp cận của bài toán này đó có thể là quy hoạch động, tham lam hoặc quay lui. Thử thách của bài toán đó là làm sao để gán các giá trị từ 1 -> n vào các node sao cho tổng của độ quan trọng là lớn nhất ?
- Một ý tưởng sơ khai đó là node nào càng có nhiều đường nối đến thì node đó phải được gán giá trị cao - đơn giản bởi vì khi tính tổng, số lần lặp lại của node này là lớn hơn so với node khác, việc cho nó giá trị lớn có thể làm tổng tăng lên đáng kể. (Cách sử dụng tham lam)
Thuật toán
Thuật toán ban đầu
- Xây dựng một dictionary $d$ tính số cạnh kết nối tới đỉnh $a_i$ và $b_i$ thông qua việc tăng lên 1 đơn vị khi duyệt qua một cạnh tại 2 đỉnh
- Sắp xếp dictionary $d$ tăng dần theo value và tạo ra một dictionary mới ($importance$) với key là key của $d$ vừa xếp và gán lần lượt giá trị 1 -> n theo thứ tự tăng dần
- Tính tổng dãy vừa tạo ra
Code mẫu được trình bày như sau :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def maximumImportance(self, n: int, roads: List[List[int]]) -> int:
d = defaultdict(int)
for road in roads:
d[road[0]] += 1
d[road[1]] += 1
sorted_nodes = sorted(d.items(), key=lambda x: x[1], reverse=True)
importance = {}
current_importance = n
for node, _ in sorted_nodes:
importance[node] = current_importance
current_importance -= 1
ans = 0
for road in roads:
ans += importance[road[0]] + importance[road[1]]
return ans
Phân tích:
- Thuật toán trên về ý tưởng là đúng và đã accept tuy nhiên vẫn còn chạy tương đối chậm với độ phức tạp \(O(NlogN)\)
- Thuật toán có thể tối ưu về bộ nhớ thông qua việc loại bỏ khởi tạo biến $importance$ và thực hiện trực tiếp trên $d$
Cải thiện thuật toán
- Thay thế dictionary thành một list thông thường từ 0 -> n - 1
- Thay thế phép tính tổng 2 $importance$ bằng tích của list vừa tính (đại diện cho số cạnh của 1 đinhr đó) với giá trị từ 1 -> n (đại diện cho giá trị importance tại đỉnh đó ) tương ứng
Code sample từ leetcode:
1
2
3
4
5
6
7
8
9
10
11
12
def maximumImportance(self, n: int, roads: List[List[int]]) -> int:
Arr = [0] * n
for A,B in roads:
Arr[A] += 1
Arr[B] += 1
Arr.sort()
summ = 0
for i in range(len(Arr)):
summ += Arr[i] * (i+1)
return summ
Phân tích:
- Độ phức tạp thời gian: \(O(NlogN)\)
- Độ phức tạp bộ nhớ: \(O(N)\) -> cải thiện hơn so với việc sử dụng 2 dictioanry
Kết luận
Đây là một bài được đánh giá là Medium nhưng mình thấy nó tương đối dễ so với các bài toán khác. Bài này chủ yếu giúp làm quen với việc sử dụng hash table sao cho hiệu quả và làm quen với đồ thị