Lời giải LeetCode Daily 29-06-2024

Giới thiệu

Thói quen mỗi ngày làm một bài leetcode daily được mình duy trì trong khoảng thời gian dài (vẫn có mấy ngày cheat day). Mình sẽ đặt vấn đề và đưa ra lời giải của mình cho bài toán, lời giải có thể hay hoặc chưa hay, mọi người có thể đưa ra nhận xét và góp ý về email của mình 😊😊😊😊. Bên cạnh đó mình sẽ phân tích thêm về sample code có tốc độ lớn của Leetcode.

Bài toán

Nguyên văn bài toán 2192 được trình bày như sau:

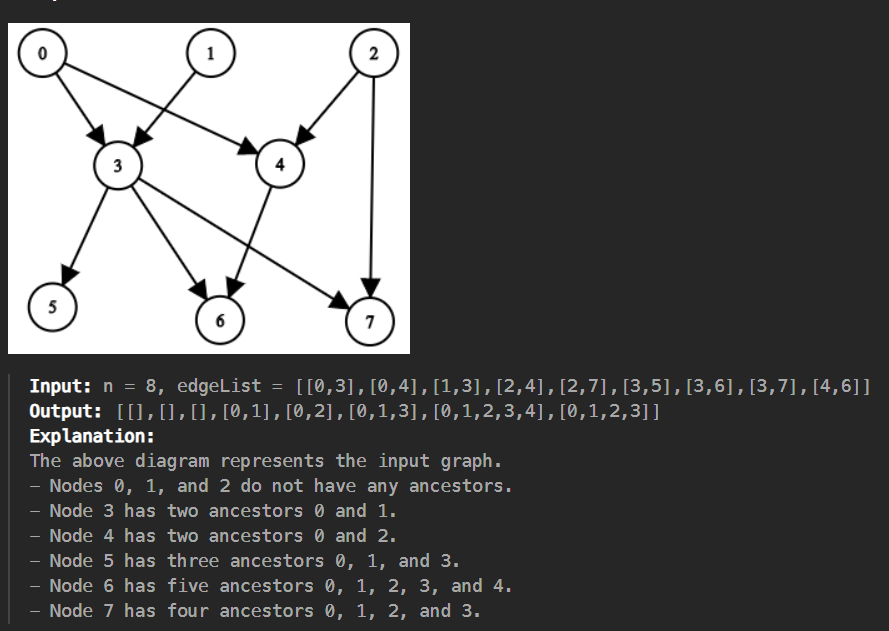
You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive). You are also given a 2D integer array edges, where edges[i] = [fromi, toi] denotes that there is a unidirectional edge from fromi to toi in the graph. Return a list answer, where answer[i] is the list of ancestors of the ith node, sorted in ascending order. A node u is an ancestor of another node v if u can reach v via a set of edges.

Bài toán được tóm tắt thành những ý sau:

1. Cho đồ thị có hướng (DAG) được gán nhãn từ 0 -> n - 1 (đồ thị biểu diễn bởi List edgeList)
2. Với mõi đỉnh, tìm tất cả các đỉnh cha của đỉnh đó

Ý tưởng

Một cách tiếp cận đơn giản nhất với bài toán này đó là liên tưởng tới thuật toán DFS tại mỗi node duyệt qua. Cụ thể thuật toán sẽ thực hiện như sau:

1. Set up bài toán với các list cần thiết : mark - list kiểu bool dùng để đánh dấu node đã duyệt, adj - ma trận kề trong đồ thị, ans - ma trận chứa đỉnh trước đó của x
2. Duyệt qua các đỉnh và thực hiện dfs trên các đỉnh đó (ví dụ bắt đầu từ đỉnh u). Tại mỗi node dfs duyệt qua, gán cho node đó có tổ tiên là u.
3. Sau khi duyệt qua tất cả các đỉnh, trả về ma trận ans.

Cài đặt thuật toán

# Python code 

def dfs(self, u: int, val: int, ances: List[List[int]], mark: List[bool], adj: List[List[int]]): 
        if not mark[u]: 
            mark[u] = True 
            if u != val : ances[u].append(val)

            for x in adj[u]: 
                self.dfs(x, val, ances, mark, adj)



    def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        ances = [[] for _ in range(n)]
        d = [0 for _ in range(n)]
        adj = [[] for _ in range(n)]

        for i in range(len(edges)): 
            adj[edges[i][0]].append(edges[i][1])

        for i in range(n): 
            mark  = [False for _ in range(n)]
            self.dfs(i, i, ances, mark, adj)

        return ances

Phân tích:

• Có thể thấy ngay, thuật toán có thể accept các test tuy nhiên chạy tương đối chậm và không quá hiệu quả
• Thực hiện dfs trên từng node và khởi tạo ma trận mark cho từng node khiến mỗi lần duyệt chạy tương đối lâu và tốn bộ nhớ. Không tận dụng được tối đa những lần duyệt
• Độ phức tạp thời gian :\(O(M + N)\)

Cải thiện thuật toán

Trong phần này mình sẽ trình bày thuật toán trong code sample của leetcode và xem mình có thể học được gì từ sample này của họ nhé ✨✨

Ý tưởng:

• Họ sử dụng thuật toán bfs kết hợp với ma trận \(indegree\) - chứa số lượng node cha trực tiếp của một node. Với mỗi lần duyệt, họ sử dụng một set để lưu giữ các node cha của nó (\(parent\)).
• Sử dụng thuật toán bfs bắt đầu với những đỉnh không có cha kề nó. Với mỗi node được lấy ra từ queue, họ duyệt qua các đỉnh kế tiếp thông qua ma trận \(adj\) (giống với ma trận \(adj\) trong ý tưởng ở trên) và sau đó update \(parent\) của nó với node lấy ra hiện tại và toàn bộ \(parent\) của node lấy ra hiện tại

Cài đặt:

    def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        adj = defaultdict(list)
        indegree = [0] * n

        for x, y in edges:
            adj[x].append(y)
            indegree[y] += 1
        
        queue = deque()
        parent = defaultdict(set)

        for i in range(n):
            if indegree[i] == 0:
                queue.append([i, set()])
        
        while queue:
            node, node_parent = queue.popleft()
            for adj_n in adj[node]:
                indegree[adj_n] -= 1
                parent[adj_n].add(node)
                parent[adj_n].update(node_parent)
                if indegree[adj_n] == 0:
                    queue.append([adj_n, parent[adj_n]])

        res = []
        for i in range(n):
            if i in parent:
                res.append(sorted(list(parent[i])))
            else:
                res.append([])
        
        return res 

Phân tích:

• Độ phức tạp thời gian :\(O(M + N)\)
• So sánh với thuật toán ban đầu có vẻ như họ đã cải thiện được các điểm yếu của mình về tốc độ và cả bộ nhớ. Việc sử dụng set thay vì khởi tạo nhiều \(mark\) tiết kiệm được tương đối bộ nhớ. Đồng thời cập nhật toàn bộ các đỉnh tổ tiên của parent vào đỉnh con là một chiến lược thông minh thay vì duyệt nhiều lần như thuật toán gốc của mình.

Kết luận

• Bài toán được đánh giá là Medium khi yêu cầu sử dụng các thuật toán duyệt đồ thị.
• Thuật toán của mình tương đối dở hơi và ngây thơ 😌😌 và cách tối ưu nó (sau khi xem sample code) thì thấy không quá khó