Lời giải LeetCode Daily 30-06-2024
Giới thiệu
Thói quen mỗi ngày làm một bài leetcode daily được mình duy trì trong khoảng thời gian dài (vẫn có mấy ngày cheat day). Mình sẽ đặt vấn đề và đưa ra lời giải của mình cho bài toán, lời giải có thể hay hoặc chưa hay, mọi người có thể đưa ra nhận xét và góp ý về email của mình 😊😊😊😊. Bên cạnh đó mình sẽ phân tích thêm về sample code có tốc độ lớn của Leetcode.
Bài toán
Nguyên văn bài toán 1579 được phát biểu như sau:
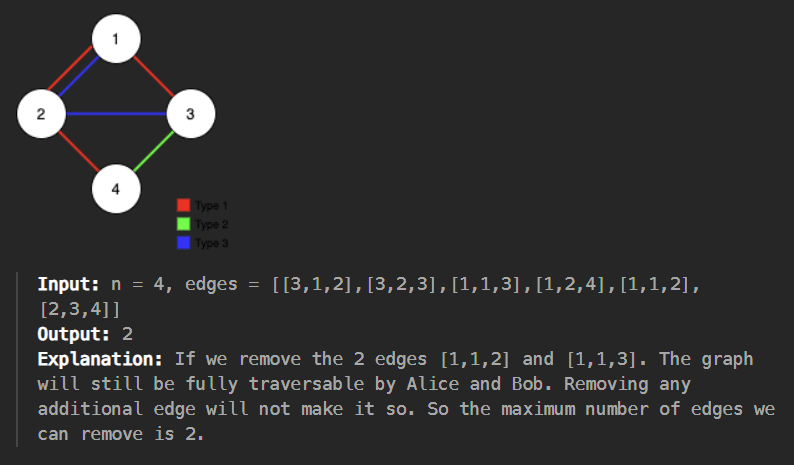
Alice and Bob have an undirected graph of n nodes and three types of edges:
Type 1: Can be traversed by Alice only. Type 2: Can be traversed by Bob only. Type 3: Can be traversed by both Alice and Bob. Given an array edges where edges[i] = [typei, ui, vi] represents a bidirectional edge of type typei between nodes ui and vi, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.
Return the maximum number of edges you can remove, or return -1 if Alice and Bob cannot fully traverse the graph.
Tóm tắt bài toán như sau:
- Có một đồ thị vô hướng với n đỉnh và 2 người A và B, các cạnh được chia thành 3 loại chính :
- Loại 1: Chỉ có A đi qua
- Loại 2: Chỉ có B đi qua
- Loại 3: Cho cả A và B đi qua
- Xóa nhiều nhất cạnh để A và B đều đi qua toàn bộ các node
Ý tưởng
Mục tiêu chính của bài toán đó là loại bỏ cạnh sao cho đồ thị vẫn có thể kết nối với nhau. Do đó một câu hỏi trong đầu được đặt ra đó là khi đỉnh thứ i nối với đỉnh thứ j làm sao để nhanh nhất kiểm tra đã tồn tại một đường nào khác nối i với j hay chưa (đường dư thừa). Một data structure nhanh chóng cho việc kiểm tra này đó là union - find
Nếu chia bài toán thành 2 điều kiện: Để A đi qua toàn bộ node và để B đi qua toàn bộ node, khi đó ta sẽ có 2 union - find. Nhiệm vụ của ta đơn giản là loại bỏ các đường dư thừa ở union - find để thỏa mãn điều kiện kết nối toàn bộ các node
Với mỗi cạnh duyệt qua, nên ưu tiên duyệt cạnh loại 3 trước, đơn giản vì cạnh này cho phép cả 2 người cùng đi qua
Thuật toán
Các bước thuật toán:
- Xây dựng Data Stucture Union - find cho mỗi người A và B
- Bắt đầu duyệt từ các cạnh loại thứ 3, kiểm tra xem cạnh nối đỉnh i và j thông qua union - find, nếu i và j đã được kết nối để tạo thành đường đi trong union-find, thực hiện loại bỏ cạnh đó
Cài đặt thuật toán:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class UnionFind:
# khởi tạo union find
def __init__(self, n: int):
self.parent = [i for i in range(n)] # đỉnh cha của tập union
self.rank = [i for i in range(n)] # size của tập union
self.count = n - 1 # kiểm tra số lượng đỉnh còn lại chưa được kết nối
# tìm kiếm đỉnh cha của node x
def find(self, x: int):
if self.parent[x] == x: return x
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
# kết nối 2 node x và y vào trong một set
def union(self, x: int, y: int):
parent_x = self.find(x)
parent_y = self.find(y)
if parent_x == parent_y: return False
self.count -= 1
if self.rank[parent_x] > self.rank[parent_y]:
self.rank[parent_x] += self.rank[parent_y]
self.parent[parent_y] = parent_x
else :
self.rank[parent_y] += self.rank[parent_x]
self.parent[parent_x] = parent_y
return True
class Solution:
def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:
# khởi tạo 2 union-find ứng với A và B
uf_a = UnionFind(n)
uf_b = UnionFind(n)
# sắp xếp để duyệt đường đi loại 3 lên trước
edges.sort(reverse=True)
ans = 0
for e in edges:
if e[0] == 3:
# nếu 2 đỉnh đã được thêm vào trong set
if not uf_a.union(e[1] - 1, e[2] - 1) or not uf_b.union(e[1] - 1, e[2] - 1): ans += 1
else:
uf_a.union(e[1] - 1, e[2] - 1)
uf_b.union(e[1] - 1, e[2]- 1)
elif e[0] == 2:
if not uf_b.union(e[1] - 1, e[2] - 1): ans += 1
else :
uf_b.union(e[1] - 1, e[2] - 1)
else:
if not uf_a.union(e[1] - 1, e[2] - 1): ans += 1
else : uf_a.union(e[1] - 1, e[2] - 1 )
if uf_a.count == 0 and uf_b.count == 0: return ans
return -1
Phân tích
- Thuật toán có độ phức tạp về thời gian là \(O(NlogN)\)
- Sử dụng cấu trúc Disjoin set giúp cải thiện việc tìm kiếm đường đi giữa 2 đỉnh bất kì đã tồn tại hay chưa
Kết luận
- Đây là bài được đánh giá là Hard tuy nhiên mình cảm thấy bài này khá dễ tiếp cận nếu bạn biết tới cấu trúc union-find. Điều khó của bài toán đó là cài đặt lại cấu trúc Union-find