Đại số tuyến tính có điều gì thú vị?

Lời nói đầu

Toán chính là nền tảng của các công nghệ, thuật toán AI nói chung và Machine Learning, Deep learing nói riêng, việc thành thạo và nắm bắt nó là vô cùng quan trọng. Để vừa học, vừa ôn lại kiến thức, mình xin giới thiệu series mới có tên Math4AI nơi mình tổng hợp các kiến thức liên quan tới các môn như Đại số tuyến tính, Giải tích, Xác suất thống kê,… dưới dạng các chuỗi series con liên quan tới từng môn học.

Mình sẽ không đưa quá nhiều kiến thức sách vở vì các bạn hoàn toàn có thể tìm thấy nó trong sách rồi mà thay vào đó các bài blog của mình hướng tới việc ứng dụng của các kiến thức đó kết hợp cùng với lý thuyết. Hy vọng mọi người sẽ có một số góc nhìn thú vị về các môn toán này. Một lần nữa, mọi nội dung mình viết có thể đúng hoặc sai và được tham khảo ở các nguồn (xem ở dưới), mọi lời góp ý của bạn đọc đều rất quý giá đối với bản thân mình, hãy liên hệ về email: gnurt17forworking@gmail.com để đóng góp nhé 🥰🥰🥰🥰

Để khởi đầu series này, mình sẽ bắt đầu một loạt các blog liên quan tới Đại số tuyến tính.

Giới thiệu bài viết

Trước khi tìm hiểu, hay học một thứ gì đó, mình luôn đặt ra các câu hỏi như: Học nó là mình đang học điều gì và điều đó giải quyết được vấn đề gì? Mình có thực sự cần phải học nó hay không và học tới mức nào là phù hợp (chuyên sâu quá hay chỉ biết thôi 🤪)?

Lướt qua những khóa học online hay các khóa học ở trên trường lớp, đều không hoặc ít cho bạn biết bạn sẽ ứng dụng mấy thứ này vào công việc, cuộc sống như thế nào (hoặc thậm chí các bạn còn không coi trong các tiết học mở đầu giới thiệu môn học), mà hầu như họ chỉ đưa ra một loạt kiến thức khô khan và bài tập để rèn luyện. Đối với mình, học mà không thể áp dụng thì nó cũng hơi lãng phí do đó, mình đi trả lời lần lượt các câu hỏi trên coi như truyền một ít cảm hứng cho mọi người về môn học thú vị này nhé.

Đại số tuyến tính là học gì?

Để hiểu được đại số tuyến tính là gì, trước hết mình sẽ đi ngay vào tên gọi của nó “Đại số tuyến tính”. Tên gọi này được chia thành 2 phần chính “Đại số” và “Tuyến tính”. Vậy thì “Đại số” và “Tuyến tính” là gì?

Đại số là nghiên cứu về các phép tính toán sử dụng các chữ cái thay thế cho những chữ số thông thường. Nghe có vẻ hơi confuse nhưng nó lại vô cùng quen thuộc, ví dụ như “\(ax^2 + bx + c = 0\)” với a, b, c, x chính là những chữ cái thay cho chữ số. Nhìn vào phương trình trên, các chữ cái thường đại diện cho một chữ số nào đó. Tuy nhiên, trong quá trình phát triển, các chữ cái còn thay thế cho những đối tượng phức tạp hơn như vector, ma trận, … Ta sẽ nghiên cứu các phép toán, quy tắc để thao tác với các kí hiệu trên, lấy ví dụ đơn giản như việc sử dụng phép nhân giữa hai ma trận, hay các quy tắc bạn sử dụng để giải một hệ phương trình được học tại phổ thông, ..

Tuyến tính tức theo mình nó đại diện cho đường thẳng, hay các mối quan hệ bậc một ví dụ như các đường thẳng bạn được học trong chương trình phổ thông. Vậy “Đại số tuyến tính” theo mình là việc mình sẽ nghiên cứu các đại lượng có quan hệ tuyến tính với nhau mà các đại lượng này có thể là vector, ma trận, … hay nói cách khác đại số tuyến tính là bạn đang nghiên cứu về các phương trình tuyến tính:

\[a_1x_1 + a_2x_2 + ... + a_nx_n = b\]

và trả lời các câu hỏi như: Làm sao để có thể tìm ra nghiệm hay giải được phương trình trên hay làm sao để biểu diễn được một đại lượng phức tạp trên thực tế, …

Nhìn phương trình trên có vẻ đơn giản nhưng nó lại được áp dụng rộng rãi vào trong rất nhiều lĩnh vực khoa học kĩ thuật tới đời sống.

Ứng dụng của đại số tuyến tính

Trong phần này, mình sẽ giới thiệu một số ứng dụng của đại số tuyến tính vào các lĩnh vực trong đời sống, đặc biệt là các lĩnh vực liên quan tới khoa học dữ liệu, học máy,..

Xử lý ảnh

Những tấm ảnh các bạn đang nhìn thấy về bản chất chính là một ma trận (mình sẽ giới thiệu sau) các pixel với 3 kênh màu RGB (đại diện cho màu đỏ, xanh lá, xanh lam)

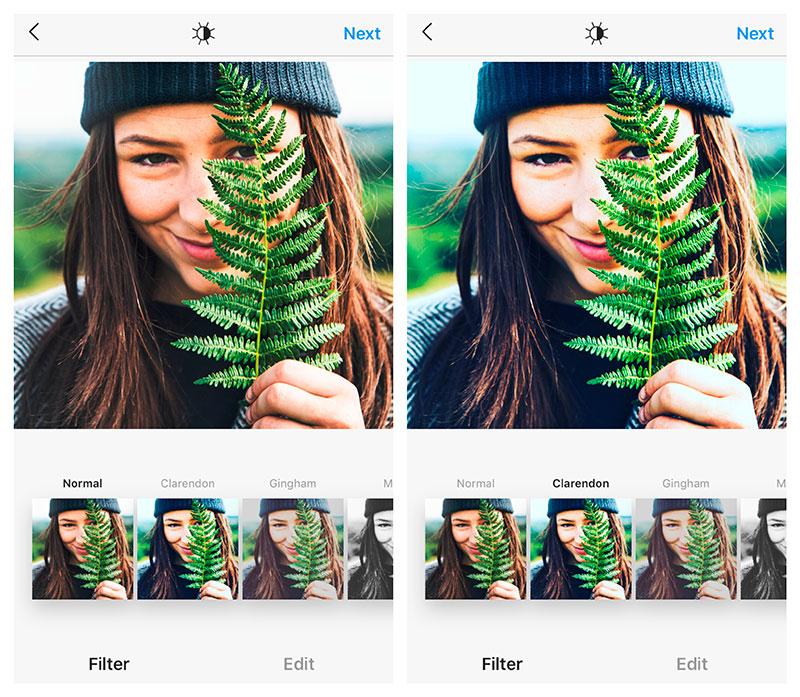
Trong máy tính, mỗi kênh màu của một điểm ảnh được biểu diễn bởi một số trong khoảng giá trị 0 - 255 (8 bits). Dựa vào cấu trúc này, có rất nhiều ứng dụng liên quan tới xử lý ảnh bản chất là sử dụng các phép tính tuyến tính liên quan tới ma trận này. Nếu là bạn hay sử dụng các bộ lọc của instagram để xử lý ảnh, đó chính là một ví dụ điển hình cho phép tích chập (convolution)

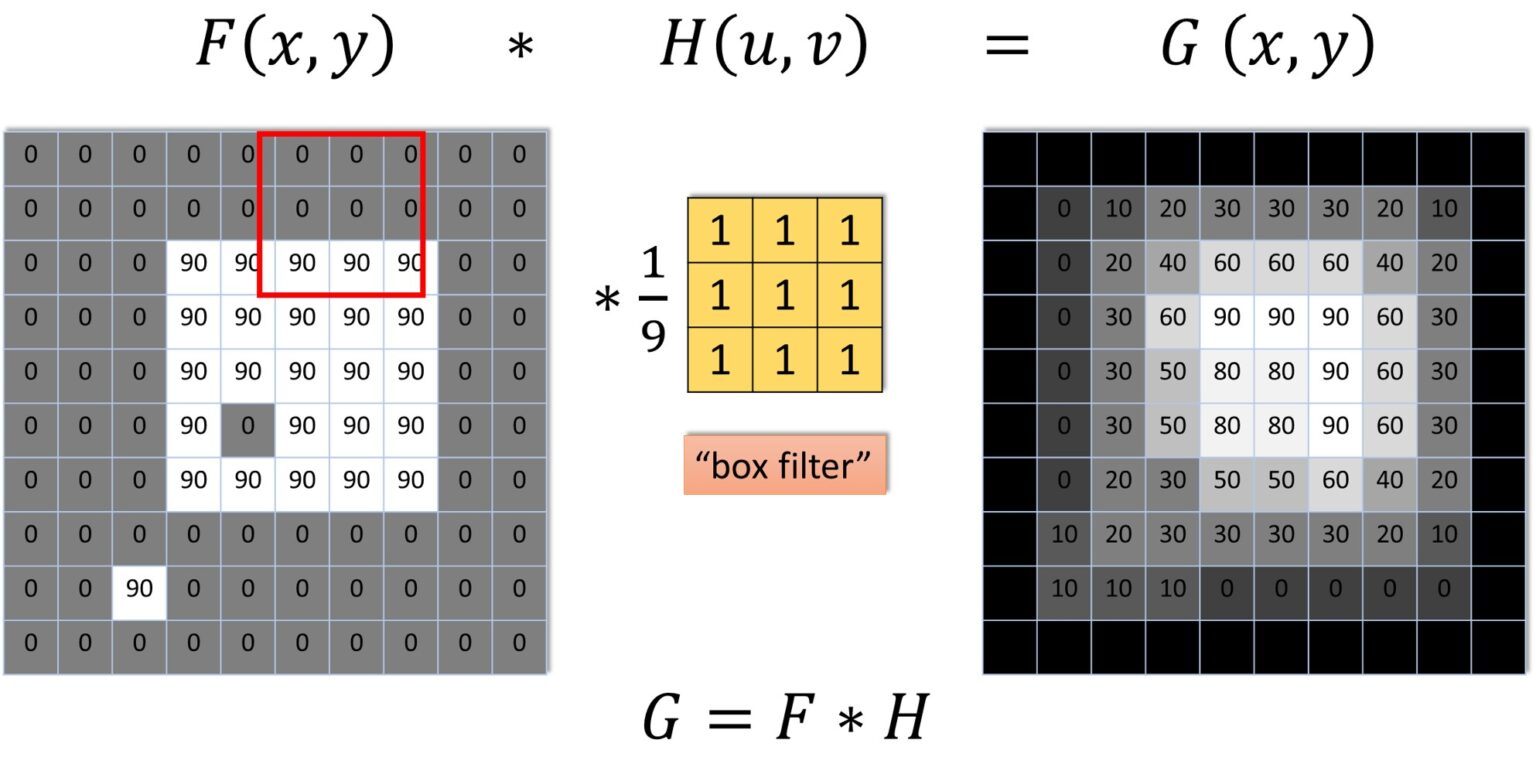
Vậy bộ lọc của instagram đã thực sự làm điều gì với ảnh? Nếu gọi ảnh gốc là một ma trận \(F(x, y)\) và ma trận lọc \(G(u, v)\) (tùy thuộc vào mỗi filter bạn thấy mà ma trận lọc này sẽ khác nhau) thì kết quả ảnh sau khi lọc sẽ là ma trận \(G(x, y)\) được tính bằng việc đặt filter lên từng hàng và tính tổng của các phần tử trong ma trận kết quả (được gọi là phép tích chập).

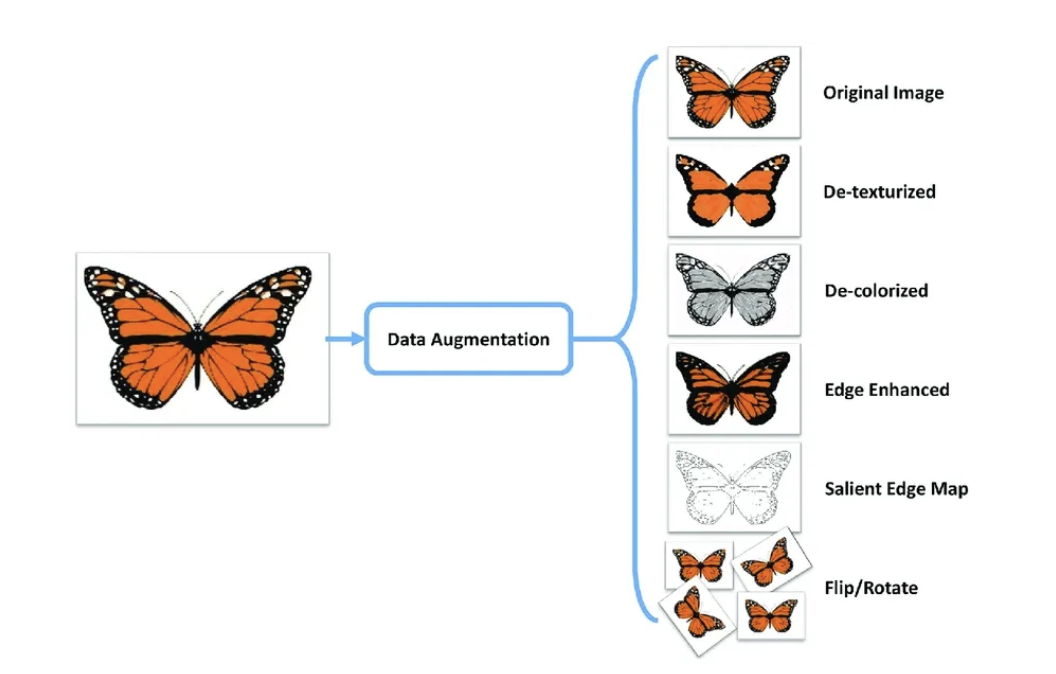
Không chỉ vậy, trong học máy, các phép xoay, lật, nhân ma trận được sử dụng như những phương pháp làm tăng tập dữ liệu (data augmentation) phục vụ cho việc huấn luyện các mô hình phức tạp đặc biệt trong lĩnh vực liên quan tới ảnh.

Biểu diễn đồ thị

Nếu bạn học ngành công nghệ thông tin, chắc hẳn bạn đã học qua môn Cấu trúc dữ liệu và giải thuật, đồ thị chính là một cấu trúc dữ liệu vô cùng quan trọng và có tính ứng dụng cao. Và bạn có nhớ có những cách nào để biểu diễn một đồ thị? Một trong những cách hiệu quả để biểu diễn một đồ thị đó là sử dụng một ma trận.

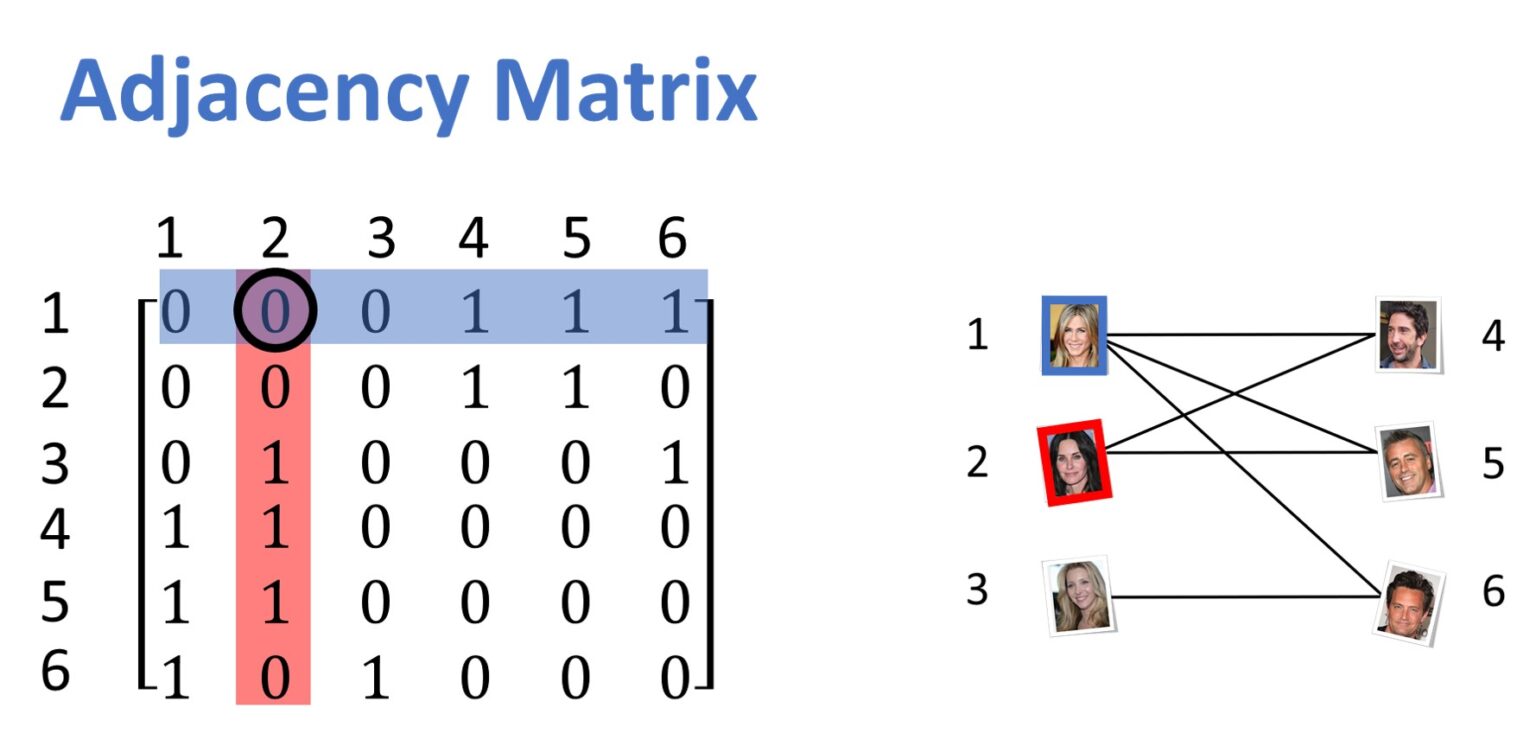
Mỗi node của đồ thị được đánh số tương ứng từ 1 -> n và biểu diễn nó thông qua một ma trận nxn chiều. Với mỗi giá trị hàng i cột j của ma trận biểu diễn cho việc người có nhãn i có kết nối với người có nhãn j hay không?. Ma trận này được gọi là một ma trận kề (adjacency matrix). Trên thực tế, dạng đồ thị này được áp dụng nhiều trong việc xây dựng các hệ thống gợi ý, đề xuất (recommendation system)

Lấy ví dụ về hệ thống gợi ý kết bạn của các mạng xã hội như Facebook hay instagram, họ luôn mong muốn trả lời được câu hỏi: Liệu người dùng A muốn kết bạn với những ai, từ đó đưa ra lời gợi ý về những lời mời kết bạn chính xác nhất. Một cách ngây thơ, nếu coi người dùng là một node trên đồ thị và mối quan hệ bạn bè giữa 2 người dùng là một cạnh thì khi đó, dữ liệu có thể được biểu diễn bởi ma trận như trên. Tuy nhiên, ma trận kề được xây dựng với một số điểm khác biệt, nó còn được gọi là ma trận utility :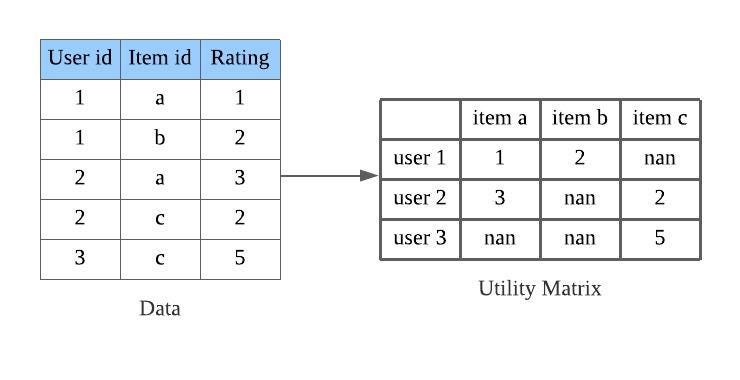

• A kết nối với B không chỉ biểu diễn bởi giá trị 1 mà biểu diễn bởi các giá trị lớn 0, giá trị này càng lớn tức A có nhu cầu kết bạn với B rất cao và ngược lại
• Giá trị 0 biểu thị A không thích kết bạn với B thay vì không có đường trực tiếp từ A tới B. Và các đường không trực tiếp này là các biến mà hệ thống mong muốn tính ra (trên hình vẽ biểu diễn bởi giá trị nan). Hay nói cách khác, bài toán hệ thống gợi ý thực chất là bài toán hoàn thiện ma trận

Ngoài ra, các bài toán liên quan đến học máy, dữ liệu thường được biểu diễn dưới dạng những ma trận vì dữ liệu thường rất lớn và có nhiều chiều (đặc biệt là dữ liệu dạng bảng). Phía trên chỉ là 2 ví dụ cơ bản nhất cho những ứng dụng của đại số tuyến tính. Do đó, nếu bạn là một người yêu thích toán, hay mong muốn theo đuổi các lĩnh vực liên quan đến học máy, khoa học dữ liệu hay thị giác máy tính,… thì đại số tuyến tính chính là nền tảng, là bước khởi đầu mà bạn nên chinh phục. Và câu hỏi cuối đó là học như thế nào là đủ, theo mình - là một sinh viên chưa tốt nghiệp, mục tiêu của mình hiện tại đó là nắm bắt và ứng dụng các kiến thức cơ bản của bộ môn này vào trong các dự án liên quan tới khoa học dữ liệu nói chung.

Kết luận

Trong bài viết này, mình đã giới thiệu qua về đại số tuyến tính nói chung, trả lời những câu hỏi mà mình đặt ra trước khi tìm hiểu về môn học này. Hy vọng đã rõ được mục tiêu và truyền một ít động lực để mọi người cùng mình chinh phục môn học này nhé. Trong các bài viết sau mình sẽ đi vào những khái niệm cơ bản nhất, tóm tắt lại những kiến thức mình đã học và diễn giải một cách rõ ràng nhất theo ý hiểu của mình. Keep practicing and studying !

Tham khảo

https://vi.wikipedia.org/wiki/%C4%90%E1%BA%A1i_s%E1%BB%91

https://vi.wikipedia.org/wiki/%C4%90%E1%BA%A1i_s%E1%BB%91_tuy%E1%BA%BFn_t%C3%ADnh

https://datahacker.rs/linear-algebra-for-machine-learning/